23.11.2025

Локализация фазударно-фрикционного взаимодействия стопы с опорной поверхностью

Между фазами ударно-фрикционного взаимодействия переднего и заднего отделов стопа находится в фазе полной опоры

Введение.

Биомеханика стопы и функция стопы различны в разных фазах фрикционного взаимодействия с опорной поверхностью [1, 2]. Между фазами ударно-фрикционного взаимодействия переднего и заднего отделов стопа находится в фазе полной опоры. Эти фазы являются объектом настоящего исследования. В работе использованы синхронизированные экспериментальные данные системы для захвата движений, предназначенной для исследования кинематики ходьбы, и динамометрической системы [3]. В эксперименте принимали участие женщины и мужчины без явных нарушений здоровья, без каких-либо травм и хирургических болезней в анамнезе, не являющиеся профессиональными спортсменами.

При моделировании биомеханики опорно-двигательной системы человека используют временные, пространственные, кинематические, динамические и другие параметры. Как правило, экспериментальной базой исследований служат методы оптических маркеров или инерциальных датчиков для получения протоколов по кинематике ходьбы. Измерения силы (в процентах от веса пациента) и времени (в процентах от цикла шага) выполняются в синхронизированном режиме на динамометрической платформе.

В работах [4, 5], посвященных динамике двуногой ходьбы, не учтены особенности локализации фаз взаимодействия стопы с опорной поверхностью. Более того, не обнаружено работ, где моделируются локальные импульсы реактивных касательных сил в фазах ударного касания пятки и носка. Не исследована фаза переката одной стопы как промежуточное ее состояние, в то время как другая стопа находится в фазе переноса.

Ударно-фрикционное взаимодействие стопы с опорной поверхностью при двуногой ходьбе.

 Есть два принципиальных соображения, чтобы выполнять парный анализ ходьбы. Во-первых, дважды в течение 20 % от цикла шага пятка одной ноги и носок другой одновременно импульсно контактируют с опорной поверхностью (двухопорный период цикла), при этом энергия взаимодействия распределяется между обеими ногами. 

Во-вторых, дважды в течение других 20 % цикла шага подошвы одной ноги в фазе ударно-фрикционного переката и полностью ступни другой в фазе свободного переноса (одноопорный период) энергия также перераспределяется между обеими ногами.

Доля полной опоры шага составляет 60 % цикла шага. При этом по 20 % приходится на три фазы:

- в первой фазе пятка одной ноги и носок другой одновременно контактируют с опорной поверхностью;

- во второй фазе одна ступня осуществляет винтовой перекат, а вторая в колебательном режиме бесконтактно переносится к точке пяточного контакта;

- третья фаза с точностью до инверсии аналогична первой фазе.

Моменты импульсов сил в локализованных фазах взаимодействия. На рис. 1 представлены фазы взаимодействия ступни с опорной поверхностью при двуногой ходьбе.

Здесь отражены только касательные взаимодействия в продольном и поперечном направлениях, формирующие процессы трения продольного скольжения и трения верчения. При этом в опорных фазах выделяют передний и задний толчки — ударные импульсы продольных и поперечных касательных сил. Эти импульсы сил локализованы, что позволило использовать при их моделировании функции Эрмита [6]:

для поперечных касательных сил

E1(t) = h1(t - m)/a exp(-(t - m)2/D,

для продольных касательных сил

E0(t) = h0 exp(-(t - m)2/D).

Здесь m — точка контакта пятки и ступни, D — дисперсия распределения, а — стандартное отклонение, ho и hi — корректирующие коэффициенты. Остановимся на рис. 1, а, на котором показано распределение касательных сил в поперечном направлении. Фазы 1 и 3 отображают одновременный ударный контакт носка и пятки. При этом, согласно экспериментам и их модельному описанию в базисе обобщенных функций Эрмита, распределения для пятки и носка являются зеркальными, в силу этого достаточно рассмотреть только один из фрагментов касательного удара. Ось абсцисс, согласно [7], используется для обозначения цикла шага, который измеряется в процентах: полный цикл — с = 100 %, а на долю полной опоры стопы приходится 60 %. Переход ко временной шкале осуществляется при задании длины шага L, скорости движения V, длины ступни l. Принято, что длина ступни равна отрезку: „пяточный бугор-плюс- но-фаланговый сустав”, а отрезки „пяточный бугор-периферия пяточной подошвы” и „пяточный бугор-дистальная фаланга” равны и обозначаются Ui. Обозначим период цикла шага Tl = L/V и зададим переменные JL/100, согласованные со шкалой цикла. В каждом отдельном случае сегменты, выражаемые в процентах, которые являются нормой для непроблемной ходьбы, пересчитываются на единицы времени. В одном из экспериментов получено Tl =0,44 с. Тогда 10 % по шкале циклов соответствует 0,044 с по шкале времени. Оба фрагмента представлены на рис. 2 для h0 = 200 (а) и h1 = 12^103 (б).

Для вычисления импульсов сил определимся с пределами интегрирования обобщенных функций Эрмита. Эти пределы выбраны таким образом, чтобы было охвачено 99 % площади под кривой функции распределения: использование правила 3а из теории вероятностей [8] дало а = 0,007 с и D = а2 = 4,9-10-5.

Вычислим импульсы сил по выражениям

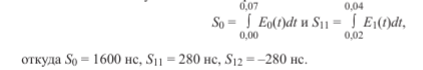
Параметры S11 и S12 представляют собой пару ударных импульсов с моментом H1 = S1U1, имеющую размерность действия, где U1 = 0,025 м. Здесь использована метрическая шкала для учета расстояния между критическими точками Е1, откуда следует H1 = 7 Дж-с.

На рис. 2, б показано распределение продольный касательных сил для обеих ступней. Рассмотрим один из фрагментов продольного касательного удара.

Вычислены S01 = 1600 нс, S02 = -1600 нс, Нз = S0U0 = 160 Дж-с. U0 — расстояние между опорными точками пятки одной ноги и носка другой в фазах их контактного ударного взаимодействия с опорной поверхностью.

Такой подход позволил установить, что при ходьбе пятка одной ноги и носок другой в первой фазе (а равно — и в третьей) формируют равные по модулю и разные по знакам моменты пар импульсов, имеющих размерность действия. Этим обеспечивается определенная нейтрализация вращения опорно-двигательной системы в условиях трения верчения. В этих же фазах продольные импульсы формируют момент пары сил только в условиях трения продольного скольжения пятки одной ноги и ступни другой.

Оценим кинетический момент тазобедренного сустава в соответствии с законами сохранения [9], используя действие в качестве меры движения.

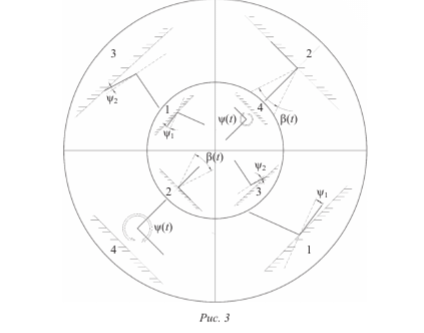
Кинематические характеристики голеностопного сустава в фазе 2. На рис. 3 представлена циклограмма шагов двуногой ходьбы в сагиттальной плоскости.

Локализованные фазы шага соответствуют квадрантам круга (секторам), которые пронумерованы начиная от фазы контакта пятки с опорной поверхностью. При этом во внешнем кольце представлены циклы шага правой ноги, а во внутреннем — левой. Есть ряд аргументов в пользу такого представления:

фазы 1, 3 и 3, 1 в смежных секторах соответствуют одновременным для обеих ног ударным импульсам пятки и носка, которые моделируются локализованным функциями Эрмита;

фазы 2, 4 и 4, 2 в смежных секторах смешанные — для одной из ног фаза переката, а для другой — фаза переноса ступни. В фазе 2 вращательно-колебательный процесс голени описывается зависимостью P(t), а в фазе 4 для контралатеральной ноги (переносная нога) наблюдается колебание ступни, которое может быть описано зависимостью y(t).

 

  Зависимости y(t) и P(t) описывают изменение во времени углов поворота ступни левой ноги в фазе свободного переноса и поворота голени правой ноги в фазе полной опоры. На рис. 4 представлены графики этих зависимостей с восходящими в одной и нисходящими — в другой области ветвями. Введем в рассмотрение усредненные угловые скорости поворота голени в фазе полного опирания и скорости поворота стопы в фазе свободного переноса:

Mir = 0,24 — угловая скорость поворота правой голени в фазе полной опоры ступни;

mil = 1,00 — угловая скорость поворота левой ступни в фазе ее переноса;

M2R = -0,82 — угловая скорость поворота правой голени в фазе полной опоры ступни;

M2l= -0,47 — угловая скорость поворота левой ступни в фазе ее переноса.

Найдем отношения величин угловых скоростей как при положительных, так и при отрицательных их значениях — К = югя/югх — коэффициент передачи: К = 0,24 для левой ветви, К2 = 1,74 — для правой. 

Приведенные значения показывают, что толчковая с носка скорость поворота ступни выше, чем финальная скорость прихода на пятку. Для голени другой ноги все наоборот.

Пациент может регулировать значения коэффициентов передачи как волево — с помощью тренировок, так и с использованием приборов, а сами коэффициенты могут служить в качестве критериев освоения навыков ходьбы [10].

Обсуждение результатов. 

Представленные расчеты отражают идеальную картину взаимодействия стопы с опорной поверхностью. В реальности модули псевдовекторов действий при верчении пятки и носка могут быть неравными; неравными могут быть и модули продольных импульсов сил, что приводит к нарушению симметрии действий при ходьбе.

Здесь стоит отметить, что дисперсия в функциях Эрмита обратно пропорциональна скорости передвижения. Указанные обстоятельства являются существенными при разработке основ проектирования ортезов голеностопного сустава [11].

Анализ ударно-фрикционного взаимодействия ступни с опорной поверхностью при двуногой ходьбе подчеркивает ритмическую моторику и это принимается как норма, к которой необходимо стремиться при реабилитации пациентов.

Заключение. 

Системность анализа двуногой ходьбы обеспечивается использованием квадросекторов шага, когда все его элементы выступают в тесной взаимосвязи друг с другом. Так, локализованные импульсы сил трения пятки одной ноги и носка ступни другой уточняют модель динамики двуногой ходьбы, позволяя использовать в качестве меры движения физическую величину — действие.

Установлены закономерности ударно-фрикционного взаимодействия ступни с опорной поверхностью в их ударных фазах. Показано, что поперечные и продольные локализованные импульсы сил формируют действия, согласованные (синхронизированные) для обеих ног.

Выявлено согласование скоростей угловых перемещений голени одной ноги и ступни контралатеральной ноги. Показано, что толчковая угловая скорость разгиба стопы превышает финальную.

Установлено, что колебательные процессы правой ступни в фазе полной опоры связаны с колебательным процессом левой ноги в фазе ее переноса посредством коэффициента передачи между значениями угловых скоростей.

СПИСОК ЛИТЕРАТУРЫ

Мусалимов В. М., Перепелкина С. Ю., Ерофеев М. А. Моделирование поперечного касательного взаимодействия стопы с опорной поверхностью // Изв. вузов. Приборостроение. 2024. Т. 67, № 10. С. 831-836. DOI: 10.17586/0021-3454-2024-67-10-831-836.

 Donatelli R. A. Normal biomechanics of the foot and ankle // J. Orthop. Sports Phys Ther. 1985. Vol. 7(3). P. 91-95. DOI: 10.2519/jospt.1985.7.3.91.

Мусалимов В. М., Паасуке М., Гапеева Е., Ерелине Я., Ерофеев М. А. Моделирование динамики опорно-двигательной системы // Научно-технический вестник информационных технологий, механики и оптики. 2017. Т. 17, № 6. С. 1159-1166.

Белецкий В. В. Двуногая ходьба: модельные задачи динамики и управления. М.: Наука, 1984. 288 с.

Вукобратович М., Франк А., Джурич Д. Об устойчивости при передвижении на двух ногах // Механика. 1972. № 1(131).

Мусалимов В. М., ЕрофеевМ. А., Монахов Ю. С., МаловМ. С. Моделирование ударно-фрикционного взаимодействия стопы с опорной поверхностью с использованием базиса обобщенных функций Эрмита // Изв. вузов. Приборостроение. 2023. Т. 66, № 8. С. 652-659. DOI:10.17586/0021-3454-2023-66-8-652-659.

Скворцов Д. В. Клинический анализ движений. Анализ походки. Иваново: Стимул, 1996. 344 с.

ФеллерВ. Введение в теорию вероятностей и ее приложения. М.: Мир, 1967. 752 с.

Лурье А. И. Аналитическая механика. М.: Физматгиз, 1961.

Письменная Е. В., Петрушевская К. А., Шапкова Е. Ю. Критерии освоения навыков ходьбы в экзоскелете у пациентов с последствиями позвоночно-спинномозговой травмы // Российский журнал биомеханики. 2018. Т. 22, № 1. С. 85.

Даминов В. Д., Зимина Е. Ю., Рыбалко Н. В., Кузнецов А. Н. Роботизированные технологии восстановления функции ходьбы в нейрореабилитации. М.: РАЕН, 2010. 128 с.

СВЕДЕНИЯ ОБ АВТОРАХ

Виктор Михайлович Мусалимов — д-р техн. наук, профессор; Институт проблем машиноведения РАН, лаборатория трения и износа; гл. науч. сотрудник

Михаил Александрович Ерофеев        — аспирант; Институт проблем машиноведения РАН, лаборатория трения и износа;

Теги: голеностопный сустав
234567 Начало активности (дата): 23.11.2025
234567 Кем создан (ID): 989
234567 Ключевые слова:  голеностопный сустав, двуногая ходьба, момент импульса, действие, квадросекторы, коэффициент передачи
12354567899