11.07.2025

Конечно-элементное моделирование анатомо-конституциональных типов позвоночно-тазового комплекса (Roussouly) в аспекте изучения их биомеханических особенностей

Сагиттальные морфотипы позвоночника Roussouly отличаются специфичностью биомеханики позвоночно-тазового комплекса (ПТК), для изучения которой в последнее время все чаще используется метод конечно-элементного (КЭ) моделирования

ВВЕДЕНИЕ

Позвоночник человека в ходе эволюции приобрел S-образную форму, оптимальную для поддержания экономичного ортостатического положения [1, 2]. Геометрическая совокупность его физиологических искривлений и таза образует цепь равновесия, согласованная работа которой пропорционально распределяет вес туловища вокруг гравитационной линии, тем самым сводя к минимуму затраты энергии и необходимость сознательного постурального контроля [3].

В 1992 г. G. Duval-Beaupere et al. ввели понятие сагиттального баланса и описали ряд рентгенометрических параметров таза, подчеркнув при этом значение его морфологии в регуляции постурального равновесия [4]. 

Исследования профильной геометрии позвоночно-тазового комплекса (ПТК) выявили значимую анатомическую вариативность позвоночника у здоровых лиц и невозможность систематизации его сагиттальной формы по средним рентгенометрическим параметрам [5]. Поэтому P. Roussouly в 2005 г. предложил выделить в нормативной популяции четыре морфологических типа ПТК с учетом наклона крестца и сагиттальной формы позвоночника [6]. В дальнейшем была выдвинута гипотеза о типоспецифичности распределения гравитационной нагрузки на различные структуры позвоночника, которая подразумевает наличие особенностей сагиттальной биомеханики и дегенерации ПТК, характерных для каждого из его морфотипов [7].

Тем не менее, необходимо отметить, что упоминаемые выводы базируются исключительно на анализе рентгенометрических параметров и соответственно носят умозаключительный характер [8]. Поэтому в последнее время популярность набирают фундаментальные исследования, направленные на объективизацию причин различных патологий позвоночника [9]. Одним из наиболее востребованных на сегодняшний день методов является конечно-элементный (КЭ) анализ, который моделирует реальную физическую систему (геометрию и условия нагрузки) с помощью математической аппроксимации [10]. Используются простые и взаимодействующие элементы (единицы), конечное число которых может быть применено для аппроксимации реальной системы с бесконечным количеством неизвестных [11]. Метод КЭ-моделирования широко практикуется в клинических исследованиях, в основном из-за воспроизводимости его результатов и низкой стоимости эксперимента [12]. КЭ-анализ может быть полезным не только в изучении этиологии дегенеративных заболеваний позвоночника, но также способствовать выявлению различных факторов, влияющих на поясничную биомеханику, в том числе геометрической вариабельности морфотипов ПТК [13].

Цель исследования — построение трехмерных реалистичных моделей, имитирующих анатомо-конституциональные типы ПТК с последующей оценкой деформативно-прочностных свойств построенных моделей при компрессионной нагрузке.

Таким образом, глубокое понимание сагиттальной биомеханики каждого из морфологических типов ПТК имеет ключевое значение в аспекте изучения патогенеза дегенеративных заболеваний позвоночника, а также прогнозирования исходов оперативных вмешательств.

МАТЕРИАЛЫ И МЕТОДЫ

КЭ-модель позвоночника строилась на основе модели, предложенной в работе Т.В. Колмаковой, Ю.А. Рикун [14]. Лордоз и кифоз позвоночника создают разную высоту межпозвонкового пространства спереди и сзади, где находится межпозвонковый диск (МПД). МПД состоит из хрящевой ткани и анатомически делится на три части. Внутренняя часть (пульпозное ядро) представляет собой гелеобразную массу, богатую водой. Наружный участок (фиброзное кольцо) имеет твёрдую и волокнистую структуру. Третья часть диска — тонкий слой гиалинового хряща, который отделяет диск от тела позвонка. Геометрическая модель включает в себя позвонки СШ (1) и CIV (2), МПД (3), фасеточные суставы (4), межостистую связку (5), задние дуги позвонков (6), остистые (7), поперечные (8) и суставные (9) отростки (рис. 1, а). В позвонках учитывается наличие губчатой (10) и компактной костной ткани (рис. 1, б).

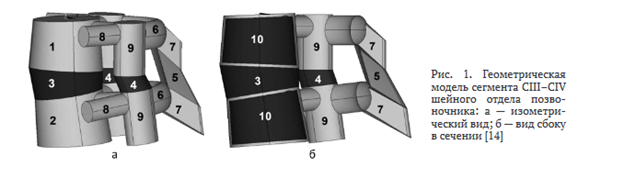
Тонкий слой кортикальной ткани охватывает тела позвонков. При выполнении моделирования считается, что позвоночные дуги и отростки позвонков полностью состоят из компактной костной ткани. Ось Z системы координат направлена вдоль оси сегмента. Ось Х направлена в переднезаднем направлении сегмента позвоночника. Учитывается наличие лордоза посредством большей высоты МПД спереди, чем сзади, или кифоза при меньшей высоте диска спереди.

Такая геометрическая модель сегментов, только с разными геометрическими параметрами, использована для КЭ-моделирования и определения напряженно-деформированного состояния грудного (ThI-ThXII) и поясничного (LI-LV) отделов позвоночника.

Костные компоненты и межпозвонковые диски объединены с использованием гексаэдрических гибридных твердых КЭ первого порядка. Коллагеновые волокна кольца и связки представлены КЭ плоской фермы (T2D2). 

Поверхности фасеточных суставов смоделированы с использованием контакта поверхность-поверхность без трения. Материал пульпозного ядра (NP) и матрицы кольца рассматривали как практически несжимаемый гиперупругий материал, который описывается законом Муни - Ривлина.

Модуль Юнга для NP измерялся в диапазоне 0,0045-1,5 МПа (v = 0,45), для гиалиновых пластин — 20 МПа (v = 0,4). Деформированное состояние коллагеновых волокон описывали нелинейной функцией зависимости напряжение-деформация. Контакт между поверхностями фасеточных суставов предполагался жестким с коэффициентом трения 0,15. Слои фасеточного хряща с начальным зазором 0,5 мм описывали как упругоизотропные (модуль Юнга 35 МПа).

Материалы кортикальной и губчатой костных тканей тел позвонков, МПД, фасеточных суставов, межостистых связок, позвоночных дуг и отростков считали изотропными линейно-упругими материалами. Механические характеристики структурных составляющих сегментов задавали в соответствии с литературными данными [15, 16] (табл. 1).

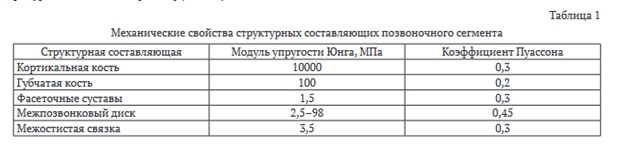
Необходимо отметить, что значения модуля упругости Юнга и коэффициента Пуассона для структурных компонентов позвоночника представлены в различных диапазонах [6].

Расчеты проводили в программном комплексе ABAOUS с использованием метода конечных элементов, задачу решали в рамках линейной теории упругости. Геометрические модели строили в соответствии с реальными размерами позвонков шейного [17], грудного, поясничного отделов [18] и МПД [19].

На основании проведенного исследования предложена следующая последовательность шагов при реализации алгоритма моделирования напряженно-деформированного состояния элементов позвоночника:

определение исходной для расчетов геометрии позвоночника тела отсчета (тело, относительно которого определяют положение заданного тела);

определение перемещения сегментов для каждого типа позвоночного столба относительно положения сегментов в теле отсчета по проекции позвоночника на вертикальную плоскость;

разбивка системы сегментов позвоночного столба на участки, которые в дальнейшем будут использованы в программе ABAOUS для формирования конечных суперэлементов, используемых для уменьшения объема вычислений в методе КЭ;

численное решение определения напряженно-деформированного состояния позвоночного столба в перемещениях, определённых в пункте 2;

определение дополнительных эквивалентных напряжений в сегментах позвоночника, вызванных смещениями относительно тела отсчета.

Исследование сходимости сетки

В настоящем исследовании рассматривали линейную гексаэдрическую сетку и восьмиузловые квадратичные тетраэдрические элементы (C3D8) для кортикальной кости, губчатой кости и задних опорных структур. Коллагеновые волокна кольца и связки представлены элементами плоской фермы (T2D2).

Проведен тест сходимости сетки, определяющий подходящее разрешение сетки КЭ-модели, для подтверждения точности моделирования. Обнаружено, что плотность сетки дает хорошую сходимость результатов с длиной стороны элемента приблизительно 1-1,5 мм. Результаты сходимости сетки показали разницу менее 5 % в нагрузках на МПД, когда количество элементов было удвоено.

Скрининг здоровой популяции осуществлялся на предмет выбора лиц с различной сагиттальной морфологией позвоночника в соответствии с пересмотренной классификацией P. Roussouly (2017) [20]. Всем согласившимся на участие в исследовании лицам выполнены профильные спондилограммы с захватом костей черепа, таза и верхней трети бедренных костей в положении стоя. После интерпретации сагиттальных параметров ПТК (Surgimap 2.З.2.1.) обследуемого он причислялся к одному из пяти типов Roussouly. В итоге отобрано 169 добровольцев: I тип — 20 человек (11,9 %), II тип — 42 человека (24,9 %), III тип — 50 человек (29,6 %); IIIA тип — 25 человек (14,7 %), IV тип — 32 человека (18,9 %). Количество больных в каждой группе усреднено до 20 человек с целью повышения соразмерности данных.

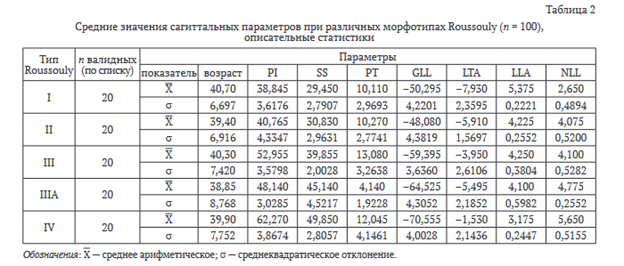
Сформированная таким образом база данных из 100 человек позволила определить диапазоны нормальных значений сагиттальных параметров (англ.: Sacral Slope — SS; Pelvic Incidence — PI; Pelvic Tilt — PT; Global Lumbar Lordosis — GLL; Lordosis Tilt Angle — LTA; Lumbar Lordosis Apex — LLA; Number (verteb) Lumbar Lordosis — NLL) для каждого из пяти морфотипов. Рентгенометрические параметры были подвергнуты стандартному статистическому анализу, который показал нормальное распределение признаков в исследуемой совокупности. В этой связи для дальнейших расчетов использовали методы параметрической статистики, а количественные параметры представляли в виде средней арифметической и стандартного отклонения (табл. 2). Таким образом, в каждой из пяти групп определены средние арифметические значения всех рентгенометрических сагиттальных параметров, совокупность которых характеризует «эталонную» профильную форму ПТК для конкретной группы, а среднеквадратичное отклонение допускало геометрические вариации морфотипов в рамках обозначенных границ. Отобранным добровольцам выполняли компьютерную томографию (КТ) ПТК для дальнейшего моделирования параметрических КЭ-моделей.

РЕЗУЛЬТАТЫ

Для изучения деформативно-прочностных свойств пяти нормальных морфотипов ПТК в соответствии с пересмотренной классификацией Roussouly разработаны параметрические КЭ-модели в среде SolidWorks. В качестве входных данных для моделирования позвоночника использовали компьютерные томограммы пяти «эталонных» добровольцев, отобранных на предыдущих этапах исследования. Построение моделей производили в соответствии с детерминантами сагиттальной морфологии ПТК, определенными P. Roussouly для каждого из пяти морфотипов [20], и рентгенометрическими параметрами «эталонных» участников исследования.

Смоделированная трехмерная модель I типа (рис. 2, а) характеризовалась низкостепенными показателями SS (29,4°) и PI (39,4°), имела короткий (NLL — 3 позвонка) поясничный гиперлордоз (GLL — (-49,5°)) с низким расположением вершины (LLA — МПД LIV-LV) и отрицательным значением LTA (-8,9°). Грудопоясничный отдел позвоночника отличался протяженным кифозом, а величина PT (10,3°) соответствовала средним значениям нормального диапазона (0-20°).

 

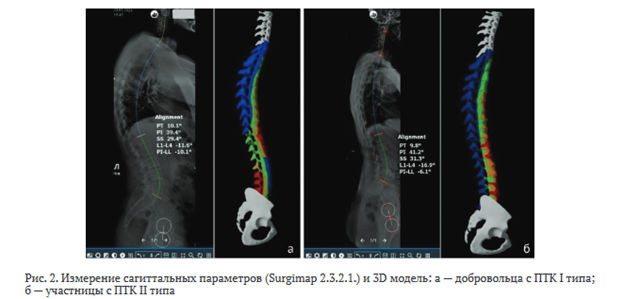
Для II типа (рис. 2, б) также характерны низкостепенные значения SS (31,3°) и PI (41,2°). Построение модели выполняли с учетом гиполордотичности (GLL — (-47,9°)) и гипокифотичности позвоночного столба, а также в соответствии с более высоким (чем при I типе) расположением LLA (центр LIV позвонка), более положительным LTA (-6,7°), большим числом позвонков в лордотической дуге (NLL — 4 позвонка) и средними значениями PT (9,8°).

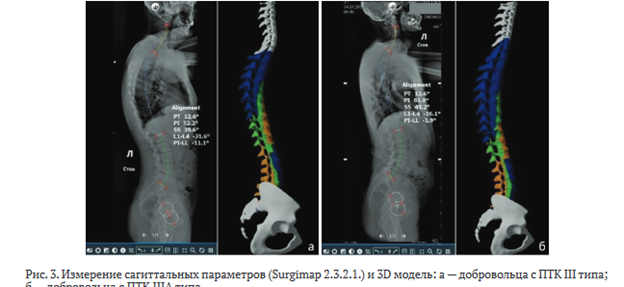
При трехмерном моделировании III морфотипа (рис. 3, а) использовали рентгенометрические параметры соответствующего «эталонного» участника: SS (39,6°), PI (52,2°) и GLL (-58,8°). Данный вариант геометрической формы характеризовался относительно длинной дугой поясничного лордоза (NLL — 4,5 позвонка), высоким расположением LLA (МПД LIII-LIV), меньшими значениями LTA (-4,5°) и средними показателями PT (12,6°).

Часть параметров, использованных для моделирования IIIA типа (рис. 3, б), были сопоставимы с таковыми при III морфологическом типе (LTA — (-6,1°); LLA — МПД LIII-LIV; NLL — 5 позвонков), однако ряд критериев имел отличия, характерные для данного морфотипа. В частности, специфичная для IIIA типа антеверсия таза PT (3,9°) обусловливала сочетание высоких значений SS (45,0°) и GLL (-65,0°) с низкими параметрами PI (48,9°).

Трехмерная модель IV (рис. 4) типа представлена гармоничным гиперизогнутым ПТК с сегментарным переразгибанием поясничного отдела. Большая величина PI (61,8°), характерная для данного сагиттального морфотипа, служила детерминантой большого наклона крестца SS (49,2°) и высокостепенного GLL (-69,8°), протяженного LLA (МПД L2-L3; NLL — 5,5 позвонков) поясничного лордоза.

 

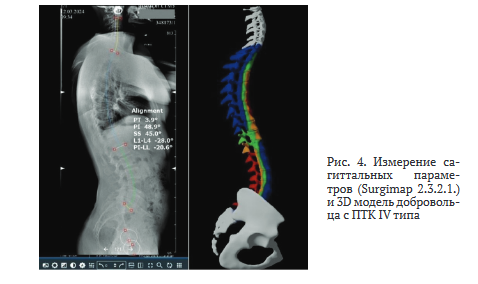
При этом LTA (-1,8°) закономерно характеризовалась близкими к 0 значениями, а PT (12,6°) находился в рамках средних значений нормального диапазона (0-20°).

Разработанные КЭ-модели пяти сагиттальных типов ПТК (по Roussouly) позволили исследовать и охарактеризовать их напряженно-деформированное состояние в условиях осевой нагрузки. В качестве граничного условия были фиксированы все узлы нижней поверхности КЭ-модели позвонка LV.

С помощью метода КЭ определены цветовые карты напряженно-деформированного состояния пяти морфотипов позвоночника. По результатам применения предложенного метода для 3Б-моделей позвоночного столба определены различные зоны напряженно-деформированного состояния позвонков: красный цвет соответствовал зоне максимальных напряжений позвонков; синий цвет характеризовал минимальные напряжения позвонков; цветовой переход обозначил воздействие напряжений на соседние позвонки.

В условиях осевой нагрузки модель I типа показала наибольшие эквивалентные напряжения по Мизесу в грудопоясничном отделе (рис. 2, а). Наиболее нагруженными оказались тела и МПД ThX-LI позвонков (2,961 МПа). В поясничном отделе наибольшие напряжения возникали на задних опорных структурах (остистые отростки, суставные отростки, ножки) а также на дорзальной части тел нижних поясничных позвонков (LIV-SI) (2,515 МПа).

Модель II типа при компрессионной нагрузке демонстрировала наибольшие эквивалентные напряжения в передних опорных структурах (тела позвонков и МПД) грудного и поясничного отделов (рис. 2, б). Поле напряжений неравномерно на протяжении указанной области, при этом наибольшие значения отмечены на уровне ThXII-LI (3,082 МПа) и LIV-LV (3,120 МПа). Задние опорные структуры позвоночника второго типа, как показывает исследование, не испытывают существенных нагрузок (0,650 МПа).

Третий тип ввиду своей геометрической сбалансированности характеризуется биомеханической стабильностью (рис. 3, а). Наиболее нагруженная зона отмечена в передних отделах грудопоясничных позвонков и МПД (ThXI-LII), а также на протяжении поясничного отдела (LI-SI): преимущественно задняя треть тел позвонков их ножки и фасеточные суставы (1,720 МПа). Тем не менее, уровень напряжений характеризовался существенно меньшими значениями по сравнению с I и II морфотипами по Roussouly (1,431 МПа).

Повышенный уровень напряжений при IIIA типе имел локализацию, характерную для III типа, однако отличался большей протяженностью границ (рис. 3, б). В частности, в грудопоясничном отделе она охватывала область с ThIX по LII позвонок, а в поясничном распространялась на задние отделы тел LIII-LV позвонков. Также следует отметить напряжения, которые превышали таковые при III типе, как в грудном (1,811 МПа), так и в поясничном отделах (1,650 МПа).

Модель IV типа демонстрировала биомеханику гиперизогнутого позвоночного столба (рис. 4). В грудном отделе при осевых нагрузках выявлены зоны с умеренным уровнем эквивалентных напряжений (2,743 МПа) по передней поверхности тел (передняя половина тел и МПД) ThIII-ThXI позвонков. Наиболее нагруженным оказался поясничный отдел, а именно задние опорные структуры LI-SI позвонков, при этом величины напряжений на остистых отростках и суставных отделах дуг имели значения, сходные с I типом (3,232 МПа).

 

ОБСУЖДЕНИЕ

В последние десятилетия отмечается существенный прогресс в изучении сагиттальной морфологии и биомеханики ПТК, оценка которых становится рутинной процедурой в диагностике и лечении различной патологии позвоночника [21]. Рядом исследователей подтверждена вариативность профильной геометрии ПТК у здоровых лиц, обосновано наличие четырех типов (с пятым подтипом в пересмотренной классификации) его нормальной профильной конфигурации и доказана типоспецифичность заболеваний. Современной тенденцией является использование воспроизводимых и доступных методик моделирования ПТК с целью объективизации причин его дегенеративной патологии [22]. Наиболее распространенным методом изучения биомеханики позвоночника in silico служит КЭ-моделирование [23]. В литературных источниках все чаще публикуют результаты различного рода испытаний, проведенных на математических моделях позвоночного столба с целью подтверждения выводов аналитических исследований [24, 25].

В настоящем эксперименте предпринята попытка изучить механические характеристики параметрических КЭ-моделей четырех классических типов ПТК и ретровертированного варианта III морфотипа, построенных на основе КТ позвоночника здоровых испытуемых со средними значениями сагиттальных параметров. Полученные результаты продемонстрировали значимое влияние профильной конфигурация пяти моделей ПТК на их сагиттальную биомеханику, что проявлялось различной реактивностью матрицы жесткости КЭ в условиях аксиальной компрессионной нагрузки. Следует отметить, что данные, полученные при изучении напряженно-деформированного состояния разработанных моделей, в большинстве случаев подтвердили теоретические закономерности, сформулированные ранее [7]. В частности, с позиции, представленной P. Roussouly концепции «контактной силы», гиполордотическая форма поясничного отдела позвоночника рассматривается в качестве основного предиктора дегенерации МПД. Последующие клинические исследования неоднократно подтвердили тот факт, что для лиц с дискогенной патологией характерны низкие значения PI, соответствующие гиполордозу [26, 27]. Изучение деформативно-проч- ностных свойств КЭ-моделей с низким PI (I и II тип) выявило зоны наибольших эквивалентных напряжений в телах позвонков и МПД преимущественно грудопоясничного (I тип — ThX-LI; II тип ThXII-LI) и поясничного (I тип — LIV—SI; II тип LIV-LV) отделов. 

Таким образом, можно сказать, что в условиях ориентации замыкательных пластин позвонков в плоскости максимально приближенной к горизонтальной, вектор гравитационной нагрузки воздействует перпендикулярно им, увеличивая тем самым перегрузку МПД. Тем не менее, следует отметить значимые напряжения на задних опорных структурах (остистые отростки, суставные отростки, ножки) в КЭ-модели I типа. Данные особенности обусловлены коротким гиперизогнутым лордозом, когда вектор биомеханического аксиального воздействия смещается на заднюю опорную колонну. В литературе имеются данные, согласующиеся с нашими выводами, в частности В. Muller проанализировал комплексные нагрузки на 28 КЭ-моделях поясничного отдела позвоночника и указал, что при гиполордотичном поясничном отделе сила сжатия воздействует преимущественно на МПД, напротив, при высоких значениях LL ее влиянию в большей степени подвержены фасеточные суставы [28]. Значимое воздействие гравитационной нагрузки на задние опорные структуры поясничного отдела позвоночника в условиях гиперлордоза подтверждают результаты, полученные нами при изучении напряженно-деформированного состояния КЭ-модели IV морфотипа. Помимо этого, область повышенных эквивалентных напряжений этой модели определена в телах и МПД на уровне грудного гиперкифоза (ThIII-ThXI). 

Интерпретируя биомеханику локальных напряжений гиперизогнутого поясничного отдела, P. Roussouly отметил, что распределение КС зависит от величины PI [7]. Чем выше значения PI, тем более наклонную ориентацию имеют позвонки, составляющие нижнюю дугу поясничного лордоза, что в свою очередь способствует распределению гравитационной нагрузки параллельно замыкательным пластинам позвонков. В данных условиях давление на МПД уменьшается, а фасеточные суставы подвергаются комбинированному воздействию: осевому (ввиду гиперэкстензии) и сдвиговому (за счет скользящей силы). С другой стороны, изучение КЭ-моделей III и IIIA типов не выявило зон механических перегрузок эквивалентных I, II и IV типам, что характеризует их геометрическую сбалансированность и биомеханическую гармоничность. Зоны умеренных напряжений как при III, так и при IIIA типе локализовались в телах и МПД грудопоясничного отдела, а также на задних опорных структурах поясничного отдела КЭ-моделей. В этой связи следует отметить ряд созвучных исследований, в которых авторы оценили напряжения и результирующие деформации вдоль позвоночного столба с помощью геометрически персонализированных КЭ-моделей и пришли к выводу, что величина PI тесно взаимосвязана с распределением сил нагрузки: при гиполордотичной форме напряжение распределяется равномерно вдоль всего позвоночника; в то время как при нормальной и гиперлордотичной конфигурации концентрация нагрузки наблюдается в основном вокруг нижней части позвоночного столба (LIII—LV) [29, 30].

Таким образом, профильная конфигурация ПТК оказывает ключевое влияние на сегментарное распределение гравитационной силы, а, следовательно, определяет специфичность сагиттальной биомеханики позвоночника, его устойчивость к динамическим нагрузкам и склонность к различной дегенеративной патологии. Как показало исследование, наиболее сбалансированными являются III и IIIA типы, при гиполордотичной форме (I и II тип) перегружаются преимущественно передние структуры позвонков, в том числе МПД, а в случае гиперлордоза (IV тип) или локальной гиперэкстензии (I тип) — задние опорные структуры.

ЗАКЛЮЧЕНИЕ

Предлагаемый алгоритм КЭ-моделирования позволяет in silico, с высокой воспроизводимостью результатов, оценить напряженно-деформированное состояние различных структур позвоночного столба. Выполненный таким образом КЭ-анализ трехмерных реалистичных моделей ПТК, построенных с учетом геометрических параметров пяти морфологических типов по Roussouly, продемонстрировал неоднозначность их сагиттальной биомеханики. Наиболее гармоничное распределение эквивалентных напряжений характерно для III и IIIA морфотипов, тогда как гипо- (I и II тип) и гиперлордотичная (IV тип) формы ПТК способствовали типоспецифичной перегрузке различных участков позвоночника. В этой связи анатомо-конституциональные особенности позвоночного столба можно считать одним из основных факторов, обусловливающих его устойчивость к динамическим нагрузкам и склонность к различной дегенеративной патологии.

СПИСОК ИСТОЧНИКОВ

Diebo BG, Varghese JJ, Lafage R, et al. Sagittal alignment of the spine: What do you need to know? Clin Neurol Neurosurg. 2015;139:295-301. doi: 10.1016/j.clineuro.2015.10.024.

Le Huec JC, Saddiki R, Franke J, et al. Equilibrium of the human body and the gravity line: the basics. EurSpine J. 2011;20(Suppl 5):558- 563. doi: 10.1007/s00586-011-1939-7.

Hasegawa K, Okamoto M, Hatsushikano S, et al. Standing sagittal alignment of the whole axial skeleton with reference to the gravity line in humans. JAnat. 2017;230(5):619-630. doi: 10.1111/joa.12586.

Duval-Beaupere G, Schmidt C, Cosson P. A Barycentremetric study of the sagittal shape of spine and pelvis: the conditions required for an economic standing position. Ann BiomedEng. 1992;20(4):451-62. doi: 10.1007/BF02368136.

Berthonnaud E, Dimnet J, Roussouly P, Labelle H. Analysis of the sagittal balance of the spine and pelvis using shape and orientation parameters. J Spinal Disord Tech. 2005;18(1):40-47. doi: 10.1097/01.bsd.0000117542.88865.77.

Roussouly P, Gollogly S, Berthonnaud E, Dimnet J. Classification of the normal variation in the sagittal alignment of the human lumbar spine and pelvis in the standing position. Spine (Phila Pa 1976). 2005;30(3):346-53. doi: 10.1097/01.brs.0000152379.54463.65.

Roussouly P, Pinheiro-Franco JL. Biomechanical analysis of the spino-pelvic organization and adaptation in pathology. Eur Spine J. 2011;20 Suppl 5(Suppl 5):609-18. doi: 10.1007/s00586-011-1928-x.

Naoum S, Vasiliadis Av, Koutserimpas C, et al. Finite Element Method for the Evaluation of the Human Spine: A Literature Overview. JFunctBiomater. 2021;12(3):43. doi: 10.3390/jfb12030043.

Коссович Л.Ю., Харламов А.В., Лысункина Ю.В., Шульга А.Е. Математическое моделирование и прогнозирование эффективности оперативного лечения в хирургии позвоночно-тазового комплекса. Вестник Самарского государственного технического университета. Серия «Физико-математические науки». 2019;23(4):744-755.

Zhang S, Bai T, Zhang X, et al. Application of Finite Element Analysis in Biomechanical Research of Degenerative Diseases of Lumbar Spine. JBM. 2022;(10):21-33. doi: 10.4236/jbm.2022.103004.

Kudo N, Yamada Y, Xiang X, et al. Concept of mathematical modeling of lumbar and thoracic spine based on elastic beam theory. JBSE. 2022;17(2):21-00331. doi: 10.1299/jbse.21-00331.

Sciortino V, Pasta S, Ingrassia T, Cerniglia D. On the Finite Element Modeling of the Lumbar Spine: A Schematic Review. Appl Sci. 2023;13(2):958. doi:10.3390/app13020958.

Cho PG, Yoon SJ, Shin DA, Chang MC. Finite Element Analysis of Stress Distribution and Range of Motion in Discogenic Back Pain. Neurospine. 2024;21(2):536-543. doi: 10.14245/ns.2347216.608.

Колмакова Т.В., Рикун Ю.А. Исследование деформационного поведения межпозвоночного диска при наклоне сегмента позвоночника. Вестник Бурятского государственного университета: Математика, информатика. 2017;(2):54-60.

Григорьев А.И., Воложин А.И., Ступаков Г.П. Минеральный обмен у человека в условиях измененной гравитации. В кн.: Проблемы космической биологии. М.: Наука; 1994;74:192-212.

Березовский В.А., Колотилов Н.Н. Биофизические характеристики тканей человека: справочник. Киев; Наук. Думка: 1990:224.

Чумаченко Е.Н., Логашина И.В. Расчет напряженно-деформированного состояния двигательного сегмента позвоночника при нагрузках. Авиакосмическая и экологическая медицина. 2014;48(5):51-57.

Tan SH, Teo EC, Chua HC. Quantitative three-dimensional anatomy of cervical, thoracic and lumbar vertebrae of Chinese Singaporeans. Eur Spine J. 2004;13(2):137-146. doi: 10.1007/s00586-003-0586-z.

Berry JL, Moran JM, Berg WS, Steffee AD. A morphometric study of human lumbar and selected thoracic vertebrae. Spine (Phila Pa 1976). 1987;12(4):362-367. doi: 10.1097/00007632-198705000-00010.

Laouissat F, Sebaaly A, Gehrchen M, Roussouly P. Classification of normal sagittal spine alignment: refounding the Roussouly classification. Eur Spine J. 2018;27(8):2002-2011. doi: 10.1007/s00586-017-5111-x.

Abelin-Genevois K. Sagittal balance of the spine. Orthop TraumatolSurgRes. 2021;107(1S):102769. doi: 10.1016/j.otsr.2020.102769.

Galbusera F, Brayda-Bruno M, Costa F, Wilke HJ. Numerical evaluation of the correlation between the normal variation in the sagittal alignment of the lumbar spine and the spinal loads. J Orthop Res. 2014;32(4):537-544. doi: 10.1002/jor.22569.

Wang W, Pei B, Wu S, et al. Biomechanical responses of human lumbar spine and pelvis according to the Roussouly classification. PLoS One. 2022;17(7):e0266954. doi: 10.1371/journal.pone.0266954.

Bassani T, Casaroli G, Galbusera F. Dependence of lumbar loads on spinopelvic sagittal alignment: An evaluation based on musculoskeletal modeling. PLoS One. 2019;14(3):e0207997. doi: 10.1371/journal.pone.0207997.

Remus R, Selkmann S, Lipphaus A, et al. Muscle-driven forward dynamic active hybrid model of the lumbosacral spine: combined FEM and multibody simulation. FrontBioengBiotechnol. 2023;11:1223007. doi: 10.3389/fbioe.2023.1223007.

Cosgun Z, Dagistan E, Dagistan Y. Effects of sagittal balance differences on spondylolisthesis. Acta Ortop Bras. 2019;27(2):120-123. doi: 10.1590/1413-785220192702205665.

Yuksel S, Ozmen E, Bari§ A, et al. Publication Trends in the Pelvic Parameter Related Literature between 1992 and 2022 : A Bibliometric Review. JKorean NeurosurgSoc. 2024;67(1):50-59. doi: 10.3340/jkns.2023.0047.

Muller A, Rockenfeller R, Damm N, et al. Load Distribution in the Lumbar Spine During Modeled Compression Depends on Lordosis. FrontBioengBiotechnol. 2021;9:661258. doi: 10.3389/fbioe.2021.661258.

Naserkhaki S, Jaremko JL, El-Rich M. Effects of inter-individual lumbar spine geometry variation on load-sharing: Geometrically personalized Finite Element study. JBiomech. 2016;49(13):2909-2917. doi: 10.1016/j.jbiomech.2016.06.032.

Filardi V, Simona P, Cacciola G, et al. Finite element analysis of sagittal balance in different morphotype: Forces and resulting strain in pelvis and spine. JOrthop. 2017;14(2):268-275. doi: 10.1016/j.jor.2017.03.007.

Информация об авторах

Алексей Евгеньевич Шульга — кандидат медицинских наук, научный сотрудник

Владимир Юрьевич Ульянов — доктор медицинских наук, заместитель директора, доцент

Юлия Юрьевна Рожкова — начальник отдела

Станислав Дмитриевич Шувалов — врач-нейрохирург

Теги: позвоночник
234567 Начало активности (дата): 11.07.2025
234567 Кем создан (ID): 989
234567 Ключевые слова:  позвоночник, сагиттальный баланс, классификация Roussouly, математическое моделирование, конечно-элементный анализ
12354567899