Цифровая модель хирургической коррекции сколиотического искривления позвоночника у детей раннего возраста

07.10.2025

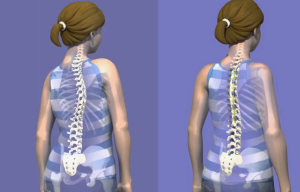
Цифровая модель хирургической коррекции сколиотического искривления позвоночника у детей раннего возраста

Коррекция врожденных деформаций позвоночника, включая аномалии формирования позвонков, остается ключевой задачей детской ортопедии

Введение

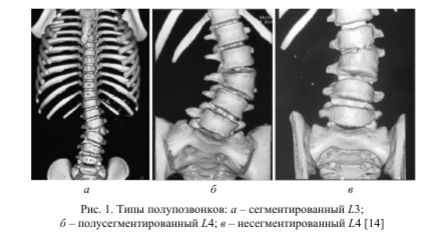
Врожденные искривления позвоночника, обусловленные нарушениями формирования позвонков [1], представляют собой сложную ортопедическую патологию, требующую особого подхода к лечению. Одной из ключевых причин таких аномалий является наличие полупозвонков, которые приводят к значительным и прогрессирующим деформациям позвоночного столба [2], вызывая болевые синдромы и прогрессирующую дисфункцию опорно-двигательного аппарата. Полупозвонки делятся на три типа: сегментированные, полусегментированные и несегментированные, что влияет на конструктивные решения при коррекции (рис. 1).

Коррекция искривления требует комплексного подхода, который включает в себя хирургическое вмешательство, направленное на восстановление нормальной оси позвоночника.

 Одним из эффективных методов, применяемых для достижения этого результата, является установка стабилизирующих конструкций, таких как транспедикулярные фиксаторы [3].

Пациенты младшего возраста особенно уязвимы к негативным последствиям операций на позвоночнике из-за повышенного риска осложнений, связанных с установкой металлоконструкций при коррекции патологии [4], что обусловлено недостаточной прочностью костных структур и их подверженностью разрушению под воздействием спинальной системы.

Успешность операции во многом зависит от предварительного анализа состояния позвоночника и сопутствующих структур [5], что подчеркивает необходимость выбора точной стратегии хирургического вмешательства.

Современные подходы к предоперационному планированию активно используют методы трехмерной визуализации, основанные на данных компьютерной томографии (КТ), что позволяет воспроизвести анатомические особенности костных структур пациента [6]. Однако существующие подходы не могут в полной мере отразить сложные биомеханические процессы, происходящие в позвоночнике под действием внешних нагрузок. В связи с этим значительно возрастает роль конечно-элементного моделирования (КЭМ), которое позволяет не только визуализировать анатомию позвоночника, но и исследовать его биомеханические свойства при различных нагрузочных условиях [7-10].

Конечно-элементный анализ предоставляет возможность оценки напряжений и деформаций, возникающих как в костных структурах, так и в имплантатах [11], что особенно важно при коррекции сложных искривлений, таких как те, что вызваны аномальными полупозвонками. Прогнозирование реакций организма, особенно в детском возрасте, имеет особое значение в клинических сценариях, где объем информации ограничен и отсутствует единая рекомендация относительно оптимального числа позвонков для фиксации.

Одним из ключевых факторов, влияющих на успешность коррекции искривлений позвоночника, является  конфигурация транспедикулярных конструкций. Количество винтов, их расположение и протяженность металлофиксации играют решающую роль в распределении механических нагрузок в имплантате. В работе Le Naveaux et al. [12] отмечается, что использование более длинных и протяженных систем фиксации может привести к нарастающему давлению на конструкцию, создавая риск перегрузки. Дополнительно, исследование Musapoor et al. показало [13], что увеличение количества транспедикулярных винтов не оказывает значительного влияния на коэффициент коррекции искривления позвоночника, что указывает на отсутствие прямой зависимости между числом винтов и эффективностью коррекции деформации. Однако стоит отметить, что увеличение плотности таких винтов приводит к значительному увеличению напряжений в области апикального позвонка, который является наиболее смещенным относительно срединной линии позвоночника. Эти выводы подчеркивают необходимость осторожного подхода к выбору фиксатора при планировании хирургических вмешательств для предотвращения повреждений конструкции [15].

Другие исследования [16-18] сосредоточены на оценке корректирующих усилий и напряжений в имплантатах, в то время как воздействие на костные структуры остается менее изученным. Это создает пробел в понимании биомеханического поведения системы «позвонки - имплантат» во время коррекции. Для достоверного прогнозирования механической стабильности системы важно учитывать не только нагрузки на эндофиксатор, но и изменения, происходящие в костных структурах.

Некоторые исследования [19; 20] предлагали подходы к моделированию коррекции искривлений позвоночника с анализом напряженно - деформированного состояния анатомических структур и имплантатов. Однако в работах использовались ограничения: отсутствие закрепления верхней и нижней частей позвоночника, что не соответствует реалистичности операции, так как другие анатомические структуры являются ограничивающими во время выравнивания позвоночника; упрощенное соединения «винт - стержень», что не позволяет анализировать полученные напряжения в стержнях [19]; отсутствие моделирования стабилизационного стержня [20]. Подобные допущения могли значительно повлиять на результат исследования. Кроме того, в обеих работах отсутствовал анализ напряжений в костных структурах.

Для достижения более точных результатов необходим комплексный подход к моделированию, включающий детализированное воспроизведение всех компонентов системы «позвонки - эндофиксатор», а также учет смежных анатомических структур и их вклада в биомеханическую стабильность позвоночника. Применение конечно-элементного моделирования с учетом всех этих факторов может значительно улучшить качество предоперационного планирования и снизить вероятность осложнений. Таким образом, разработка цифровой модели операции с использованием конечно-элементного моделирования для оценки поведения биологических и имплантируемых структур при коррекции искривления позвоночного столба представляет собой важный шаг в повышении эффективности и безопасности хирургических вмешательств.

Материалы и методы

В Национальном медицинском исследовательском центре детской травматологии и ортопедии имени Г.И. Турнера поставлена задача исследования структур позвоночного столба и имплантата во время выполнения исправления деформации позвоночника у детей раннего возраста.

В данной работе рассматривается случай трехлетнего пациента с выраженным сколиозом в 34° по Коббу. На основании данных компьютерной томографии разработана конечно-элементная модель сегмента Th 12-S1. Основная задача работы заключается в исследовании напряженно-деформированного состояния биомеханической системы «позвонки - эндофиксатор» во время исправления искривления позвоночного столба.

Хирургическая тактика коррекции искривления позвоночника

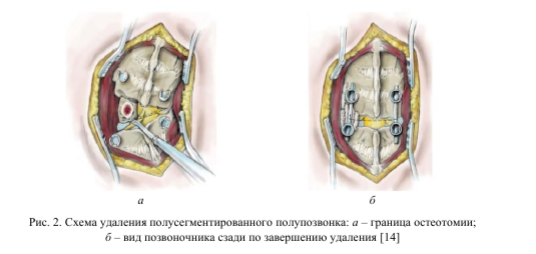
Хирургическое устранение искривления на фоне аномального полупозвонка проводится по следующему принципу: после удаления тела аномального позвонка в сформированные костные каналы соседних интактных позвонков, относительно аномального полупозвонка, устанавливаются транспедикулярные винты; затем выполняются корригирующие манипуляции в виде стягивания позвонков вдоль стержня, который следует естественным изгибам позвоночника, и фиксируется в головках винтов, начиная с выпуклой стороны искривления; после этого на вогнутой стороне искривления проводится дистракция (раздвижение) интактных позвонков вдоль стержня с использованием винтов в качестве опоры (рис. 2) [3]

Преобразование данных компьютерной томографии

Последовательность преобразования данных компьютерной томографии пациента Н. для создания конечно-элементной модели и проведения моделирования выравнивания позвоночного столба представлена на рис. 3.

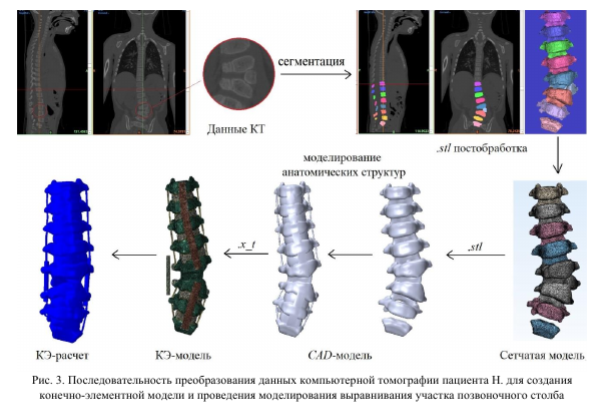
Данные компьютерной томографии (КТ аппарат Philips Brilliance, 64 среза) пациента Н. в возрасте трех лет до операции импортированы в формате DICOM в программный пакет Mimics 21.0 (Materialise, Левен, Бельгия) для сегментирования костных структур участка Th 12-S1. Протяженность выбранного участка обусловлена количеством позвонков, вовлеченных в сколиотическое  искривление.  Аномальный полупозвонок располагается между позвонками L4-L5. В данном случае наблюдается люмбализация - врожденный порок развития позвоночника, сопровождающийся формированием дополнительного позвонка, в данном случае L6. Крестец состоит из несросшихся позвонков.

Постобработка сеток позвонков Th12-S1 в программном обеспечении 3-Matic 13.0 (Materialise, Левен, Бельгия) в формате STL подразумевала создание однородной сетки с ребром 0,25 мм. На данном этапе происходит разделение костной ткани на кортикальную и губчатую составляющие - толщина кортикального слоя 0,6 мм, согласно данным КТ.

Полученные сетчатые модели позвонков участка позвоночного столба Th12-S1 импортированы в программный пакет SolidWorks 2020 (Dassault

Systemes, Франция) в формате STL для создания твердотельных объектов с ^^KBS-поверхностями с помощью расширения Scanto3D. Следующим этапом является моделирование анатомических структур связочного аппарата, дисков, фасеточных суставов и имплантата.

Модель импортируется в программный пакет Abaqus 2021 (Dassault Systemes, Франция) в формате Parasolid (.x_t) для создания конечно-элементной модели и проведения моделирования выравнивания участка позвоночного столба.

Геометрическая модель участка позвоночника Th 12-S1

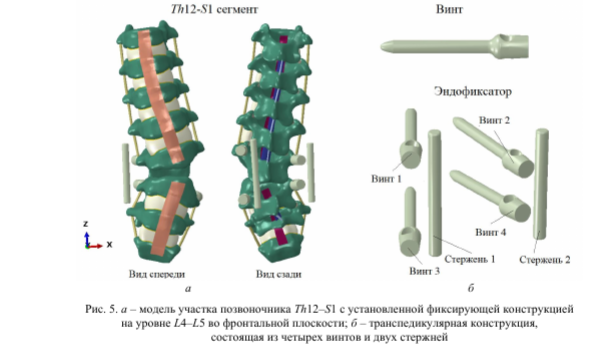
Более подробное представление достроенных анатомических структур и фиксирующей конструкции представлено на рис. 4, 5. Согласно атласу анатомии человека [21], построена модель связочного аппарата позвоночного столба, состоящего из передней продольной связки, задней продольной связки; межпоперечной связки; межостистой связки и желтой связки. Межпозвоночные диски состоят из пульпозного с ядра, фиброзного кольца и замыкательных пластинок. Модели фасеточных суставов представлены нижней и верхней частями в соответствии с анатомическим описанием соответствующих прилежащих позвонков [22].

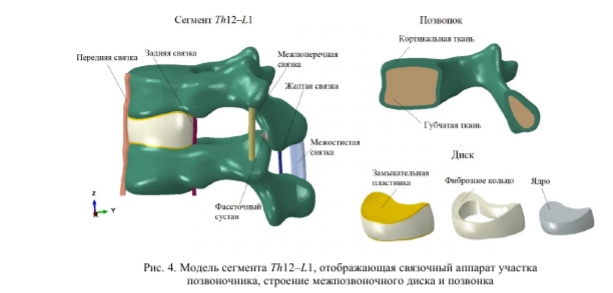
Стоит отметить, что при моделировании участка позвоночного столба Th12-S1 до реконструкции удалены полупозвонок и прилегающие межпозвоночные диски и связки в зоне аномалии согласно этапу операции, для мобилизации, условно разделенной верхней и нижней частей позвоночника.

Транспедикулярный эндофиксатор, состоящий из двух стержней и четырех винтов, смоделирован на основе доступных данных, полученных в процессе исследования. Геометрия винта представлена в упрощенном виде без резьбовой нарезки [23]. Отверстие в головке винта совпадает с геометрией стержня. Пространственное положение стержней определено на основе послеоперационного КТ.

Конечно-элементная модель участка позвоночника Th12-S1

Контактное взаимодействие для всех компонентов, за исключением фасеточных суставов и контактной пары «винт - стержень»,ограничено парным поверхностным   контактом. 

Верхней и нижней поверхностям суставных отростков задан коэффициент трения равным 0,05. Для контактной пары «винт - стержень» задан коэффициент трения равным 0,3.

Для структур связочного аппарата построена 8-узловая гексаэдральная сетка C3D8  - всего 83 979 элементов, для фиброзного кольца и пульпозного ядра - 4-узловая тетраэдральная сетка с гибридными элементами C3D4H - всего 322 714 элементов, для остальных структур - 4-узловая тетраэдральная сетка C3D4 - всего 1 872 450 элементов.

 Размер элемента: связки и фасеточные суставы - 0,22 мм; фиброзное кольцо, пульпозное ядро, концевые пластины - 0,7 мм; кортикальная и губчатая ткани - 1,2 мм (в позвонках L4-L5-1 мм); винты - 0,42 мм (зона контакта «винт - стержень», внутренняя область винта - 0,19 мм); стержни - 0,385 мм.

Механические свойства материала

Предполагается, что материал компонентов сплошной, упругий, изотропный, за исключением межпозвоночного диска (гиперупругий материал, описанный моделью Муни - Ривлина) и эндофиксатора (изотропный упругопластичный материал [24]). Механические свойства материалов (E - модуль упругости; v - коэффициент Пуассона; От - предел текучести; Ci0, C0i - константы в модели Муни - Ривлина [25]) участка позвоночника TM2-S1 представлены в табл. 1. Для оценки напряжений в кортикальной и губчатой костях предел текучести был усреднен на основании данных, приведенных в работах [26-29].

Принципы нагружения в ходе коррекции деформации позвоночника

В данном разделе описывается последовательность этапов нагружения биомеханической системы «позвонки - эндофиксатор» в процессе коррекции сколиотического искривления.

Моделирование нагружения системы проводится с учетом этапов операции по коррекции сколиотического искривления. В начальный момент удаляются аномальные структуры (полупозвонок, прилегающие диски и связки), после чего устанавливаются транспедикулярные винты в соседние тела позвонков. Далее проводится коррекция искривления за счет смещения и поворота позвонков относительно винтовой системы (табл. 2). Основное внимание в расчетах уделено распределению напряжений в костных структурах и эндофиксаторе при корректирующих манипуляциях.

В процессе моделирования биомеханической системы для коррекции сколиотического искривления используется кинематическая связь, которая позволяет учитывать смещения и повороты позвонков относительно фиксирующих элементов. Эта связь задается между головками винтов и геометрическими центрами позвонков для обеспечения точного моделирования движения в процессе коррекции.

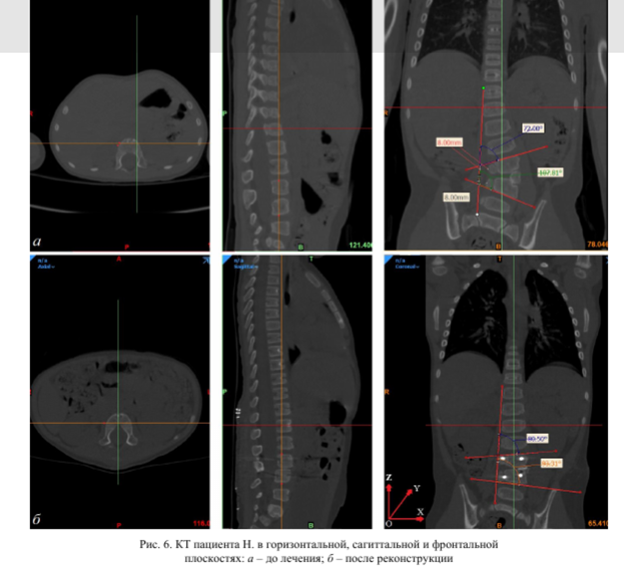
Выравнивание сколиотического искривления производится относительно позвонков 7Ы2 и <S1 путем смещения винтов, установленных в костные компоненты L4-L5. На основе КТ до и после реконструкции (рис. 6) определены смещения и повороты позвонков: для L4 вдоль оси ОХ 8 мм, угол поворота 8,5°, относительно оси ОУ; для L5 вдоль оси ОХ 8 мм, угол поворота 14,5°, относительно оси ОУ.

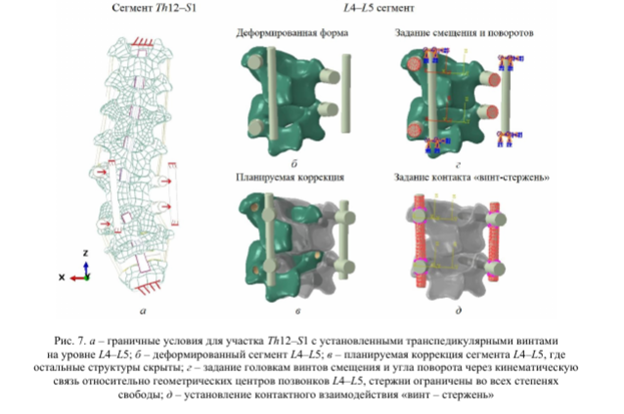
Верхняя концевая пластина 7Ы2 и нижняя концевая пластина <S1 жестко закреплены. Верхняя и нижняя части стержней ограничены во всех степенях свободы (рис. 7, а). На рис. 7, б и в, представлена деформированная форма участка L4-L5 и планируемая коррекция.

После выполнения всех этапов моделирования нагружения биомеханической системы «позвонки - эндофиксатор» получены результаты, позволяющие оценить напряженно-деформированное состояние как костных структур, так и имплантата.

 

 Результаты

Получены результаты расчета напряженно - деформированного состояния структур в биомеханической системе «позвонки - эндофиксатор». Проведена сравнительная оценка формы искривления позвоночника на начальном этапе моделирования и по его завершении с данными компьютерной томографии пациента Н. до и после хирургического вмешательства (рис. 8). До операции сколиотическая дуга составляла 34°, после - 6,1° по данным КТ при измерении по Коббу. В моделировании после выравнивания сегмента Th 12-51 сколиотическая дуга уменьшилась до 5,9°.

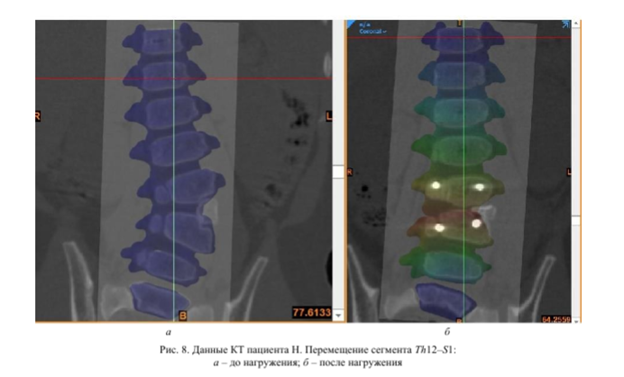
Разница величин составила 3,2 %.

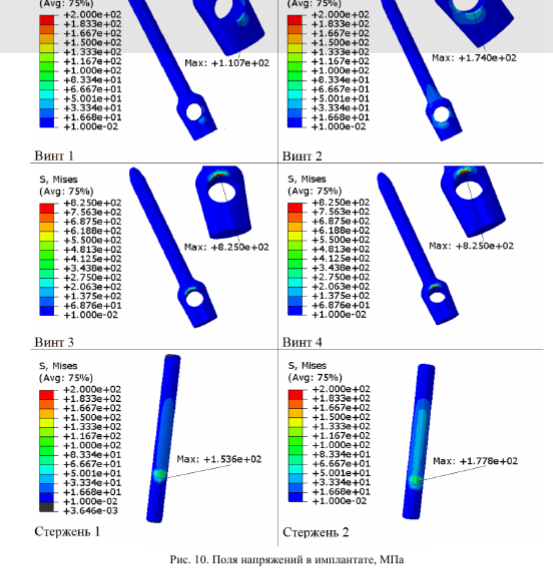
В работе оценивались значения напряжений в костных структурах (рис. 9) и имплантате (рис. 10) во время исправления сколиотической дуги (конец пятого шага расчета). Максимальные напряжения в сегменте L4-L5 представлены в табл. 3.

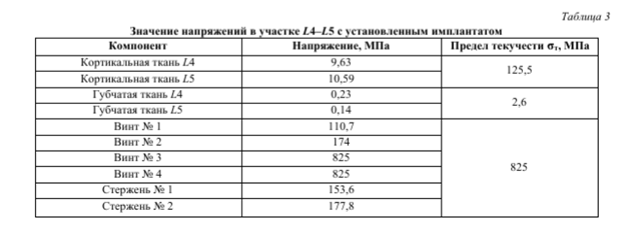
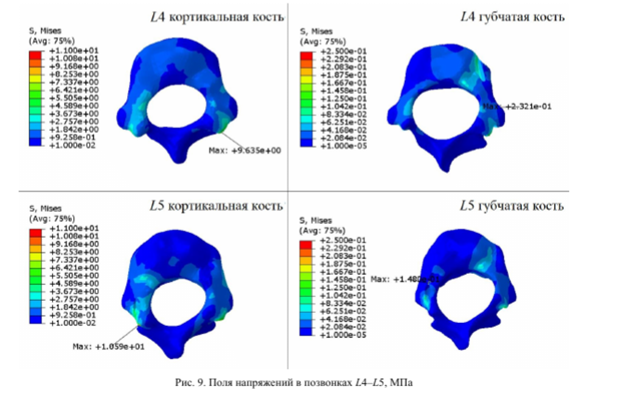
Полученные результаты требуют более детального анализа для глубокого понимания поведения системы во время коррекции. Основываясь на этих данных, можно сделать выводы о распределении напряжений в костных структурах и имплантатах, а также оценить влияние этих факторов на механическую стабильность конструкции в процессе хирургического вмешательства.

Обсуждение

Проведенный конечно-элементный анализ позволил оценить биомеханическое поведение системы «позвонки - эндофиксатор» при коррекции сколиотической деформации. 

Выявлено, что при моделировании коррекции сколиотической дуги напряжения в костных структурах остаются в пределах нормы. Наибольшее нагружение во время коррекции испытывает позвонок L5 в области контактного взаимодействия «винт № 3 - кортикальная кость», это объясняется близким расположением позвонка L5 к месту защемления нижней концевой пластины М, относительно которой и происходит выравнивание. При анализе губчатых тканей позвонков максимальное напряжение наблюдается в позвонке L4 в области контакта «винт № 2 - губчатая ткань». Можно предположить, что данный результат связан с особенностями установки транспедикулярного винта, так как винт № 2 располагается вблизи границы губчатой и кортикальной тканей. Распределение напряжений в позвонках согласуется с данными об уязвимости тел позвонков после установки опорных элементов и выполнения корректирующих действий [36; 37].

Среднее значение напряжения в фиброзном кольце межпозвоночного диска составляет 1,24 МПа, что соответствует приведенным данным в работе [20].

Анализ результатов в имплантате показал, что наибольшие значения напряжений концентрируются в зоне контакта «винт - стержень». В винтах № 3 и № 4 - позвонок L5 в зоне соединения со стержнем наблюдаются локальные пластические деформации, вызванные достижением принятого предела текучести титанового сплава. В более раннем способе коррекции сколиоза с помощью транспедикулярного фиксатора использовались прямые стержни. 

Задача хирургов заключалась в том, чтобы во время операции согнуть стержни согласно физиологическому изгибу позвоночника в оперируемой области [38]. Соответственно стержень, принимая новую форму, подвергался пластической деформации в местах изгиба. Безусловно, такой интраоперационный изгиб может вызвать необратимые деформации в материале, что впоследствии отразится на прочности стержневой конструкции, снижая предел текучести и жесткость [39]. В ряде работ [40;  41] сообщается о послеоперационной деформации стержней, которая возникает в результате коррекционных маневров. Что касается поведения транспедикулярных винтов, то в клинических и экспериментальных исследованиях сделан вывод, что винты могут испытывать пластические деформации без возникновения перелома [42]. Приведенные данные говорят о возможности титанового сплава выдерживать высокие нагрузки, при этом не разрушаясь. Следовательно, подобное локальное напряжение в винтах № 3 и № 4 может говорить об ограниченной деформации, которая не приведет в дальнейшем к поломке фиксатора. Однако произошедшие изменения механических свойств имплантата могут повлиять на его прочность в перспективе. В остальной части имплантата напряжения не превышают предела текучести. Значения напряжений в стержнях близки к данным работы, в которой проводилась оценка значений напряжений при различных стратегиях коррекции искривления позвоночника [43].

Стоит отметить, что решение контактной задачи является непростым процессом в конечно-элементном анализе. Одним из основных факторов влияния на результат является геометрия контактной области [44]. Расчетная сетка в области интереса должна быть высокого качества и содержать элементы правильной формы [45]. При наличии острых кромок в геометрии может наблюдаться концентрация напряжений в этой области [46]. При моделировании винтов с отверстиями для стержней мы столкнулись со сложностями сходимости сетки в зоне контакта «винт - стержень». Даже при изменении размера элемента, исчисляемого в сотых долях миллиметров, в контактной области могли наблюдаться значительные колебания результатов возле кромок отверстия. Экспериментальным путем найден оптимальный размер элемента 0,19 мм для внутренней поверхности винта, который соединяется со стержнем. Вероятнее всего, данная проблема связана с геометрией отверстия в головке винта, предназначенного для укладывания стержня. Влияние размера элемента сетки на концентрацию напряжений подтверждается в работе [47]. Это говорит о том, что подобные результаты исследований необходимо интерпретировать с осторожностью.

Одним из ограничений проведенного моделирования является отсутствие учета мышц позвоночного столба, которые влияют на общую жесткость позвоночного сегмента [48]. В ряде исследований подобное исключение являлось допустимым [49-51]. Возможно, в будущих исследованиях мы проведем анализ целесообразности включения мышечного аппарата в модель. Также стоит отметить, что физические свойства биологических структур у детей имеют значительную вариабельность. Что касается костных структур, в работе [52] предложен метод определения механических свойств тканей на основе связи рентгеновской плотности и модуля упругости. В последующих работах мы бы хотели применить предложенный способ расчета для конкретного пациента и оценить его влияние на результат напряжений и деформаций.

Данная модель является первым этапом для ответа на вопрос по поводу оптимальной протяженности фиксации сегментов при коррекции врожденной деформации позвоночника в зависимости от степени искривления. В последующих исследованиях будут проведены сравнительные  КЭ-расчеты биомеханической системы «позвонки - эндофиксатор» при разных величинах деформации позвоночного столба.

Заключение

Разработана цифровая модель биомеханической системы «позвонки - эндофиксатор», которая продемонстрировала высокую точность в прогнозировании  напряженно-деформированного состояния при исправлении сколиотического искривления.

Выявлено, что при коррекции сколиотической деформации 34° по Коббу напряжения в костных структурах при установке транспедикулярной конструкции на два интактных позвонка не превышают предельного значения. В установленных винтах в нижний позвонок L5 в зоне контакта «винт - стержень» наблюдались локальные необратимые деформации. Данные области могут быть более уязвимы, при дальнейшей эксплуатации имплантата, что необходимо учитывать. Полученные результаты напряжений в межпозвоночных дисках и стержневых структурах согласуются с работами других авторов. Сравнительный анализ сколиотической дуги до и после реконструкции в модели и согласно данным КТ выявил отличие результатов в 3,2 %, что является адекватным значением.

Полученные результаты моделирования предоставляют важные сведения, которые могут быть использованы для улучшения предоперационного планирования и повышения надежности имплантатов при лечении врожденных искривлений позвоночника у детей. В дальнейшем использование таких цифровых моделей может способствовать разработке новых методов хирургической коррекции с учетом индивидуальных анатомических особенностей пациента, что особенно важно для минимизации рисков осложнений и улучшения долгосрочных результатов

Список литературы

Taragin, B.H. The spine: congenital and developmental conditions / B.H. Taragin, S.L. Wootton-Gorges // Pediatric Orthopedic Imaging. - 2014. - P. 43-105.

3D analysis of congenital scoliosis due to hemivertebra using biplanar radiography / L. Humbert, J.S. Steffen, R. Vialle, J.  Dubousset, J.M. Vital, W. Skalli // European Spine Journal. - 2013. - Vol. 22. - P. 379-386.

Особенности использования интраоперационного нейрофизиологического мониторинга при дорсальной резекции полупозвонков / С.В. Виссарионов,

А.Р. Сюндюков, Н.С. Николаев, В.А. Кузьмина, П.Н. Корняков, М.Н. Максимов, И.В. Михайлова // Ортопедия, травматология и восстановительная хирургия детского возраста. - 2021. - Т. 9, № 3. - С. 267-276.

Causes of the failure and the revision methods for congenital scoliosis due to hemivertebra / Z. Shi, Q. Li, B. Cai, B. Yu, Y. Feng, J. Wu, B. Ran // Congenital Anomalies. - 2015. - Vol. 55, no. 3. - P. 150-154.

The efficacy and complications of posterior hemivertebra resection / J. Zhang, W. Shengru, G. Qiu, B. Yu, W. Yipeng, K. D. Luk // European Spine Journal. - 2011. - Vol. 20, no. 10. - P. 1692-1702.

Optimal surgical planning guidance for lumbar spinal fusion considering operational safety and vertebra-screw interface strength / J. Lee, S. Kim, Y.S. Kim, W.K. Chung // The International Journal of Medical Robotics and Computer Assisted Surgery. - 2012. - Vol. 8, no. 3. - P. 261-272.

Исследование прочности эндопротеза тазобедренного сустава из полимерного материала / Л.Б. Маслов, Ю. Дмитрюк, М.А. Жмайло, А.Н. Коваленко // Российский журнал биомеханики. - 2022. - Т. 26, № 4. - С. 19-33.

Real-time biomechanics using the finite element method and machine learning: Review and perspective / R. Phellan, Hachem, J. Clin, J.M. Mac-Thiong, L. Duong // Medical Physics. - 2021. - Vol. 48, no. 1. - P. 7-18.

Конечно-элементный  анализ напряженнодеформированного состояния эндопротеза тазобедренного сустава при ходьбе / Л.Б. Маслов, А.Ю. Дмитрюк, М.А. Жмайло, А.Н. Коваленко // Российский журнал биомеханики. - 2021. - Т. 25, № 4. - 414-433.

From finite element meshes to clouds of points: a review of methods for generation of computational biomechanics models for patient-specific applications / A. Wittek, N.M. Grosland, G.R. Joldes, V. Magnotta, K. Miller // Annals of biomedical engineering. - 2016. - Vol. 44. - P. 3-15.

Stress distribution in vertebral bone and pedicle screw and screw-bone load transfers among various fixation methods for lumbar spine surgical alignment: a finite element study / M.   Xu, J. Yang, I. Lieberman, R. Haddas // Medical Engineering and Physics. - 2019. - Vol. 63. - P. 26-32.

How does implant distribution affect 3D correction and bone- screw forces in thoracic adolescent idiopathic scoliosis spinal instrumentation? / F. Le Naveaux, A.N. Larson, H. Labelle, X. Wang, C.E. Aubin // Clinical Biomechanics. - 2016. - Vol. 39. - P. 25-31.

Musapoor, A. A finite element study on intra-operative corrective forces and evaluation of screw density in scoliosis surgeries / A. Musapoor, M. Nikkhoo, M. Haghpanahi // Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. - 2018. - Vol. 232, no. 12. - P. 1245-1254.

Картавенко, К.А. Хирургическое лечение детей с врожденной деформацией позвоночника при полупозвонках поясничного отдела: дис. ... канд. мед. наук / К.А. Картавенко. - СПб., 2017. - 177 с.

Biomechanical analysis of correction force and Cobb angle in a simple model of scoliotic spine fixation / M. Rusli, N.   K. Putra, H. Dahlan, R.E. Sahputra // AIP Conference Proceedings. - 2019. - Vol. 2187, no. 1. - P. 050022.

Relationship of forces acting on implant rods and degree of scoliosis correction / R.A. Salmingo, S. Tadano, K. Fujisaki, Y. Abe, M. Ito // Clinical Biomechanics. - 2013. - Vol. 28, no. 2. - P. 122-128.

Scoliosis corrective force estimation from the implanted rod deformation using 3D-FEM analysis / Y. Abe, M. Ito,K.  Abumi, H. Sudo, R. Salmingo, S. Tadano // Scoliosis. - 2015. - Vol. 10. - P. 1-6.

Biomechanical analysis of corrective forces in spinal instrumentation for scoliosis treatment / X. Wang, C.E. Aubin, H. Labelle, S. Parent, D. Crandall // Spine. - 2012. - Vol. 37, no. 24. - P. E1479-E1487.

Planning the surgical correction of spinal deformities: toward the identification of the biomechanical principles by means of numerical simulation / F. Galbusera, T. Bassani,

La Barbera, C. Ottardi, B. Schlager, M. Brayda-Bruno, T. Villa, H.J. Wilke // Frontiers in Bioengineering and Biotechnology. - 2015. - Vol. 3. - P. 178.

Development of a detailed volumetric finite element model of the spine to simulate surgical correction of spinal deformities / M. Driscoll, J.M. Mac-Thiong, H. Labelle, S. Parent // BioMed Research International. - 2013. - Vol. 2013. - P. 931741.

Липченко, В.Я. Атлас нормальной анатомии человека / Я. Липченко, Р.П. Самусев. - М.: Медицина, 1989. -18-30.

Improvement and validation of a female finite element model of the cervical spine / A.J. Silva, R.J.A. de Sousa, F.A. Fernandes, M. Ptak, M. Dymek, M.P. Parente // Journal of the Mechanical Behavior of Biomedical Materials. - 2023. - Vol. 142. - P. 105797.

La Barbera, L. Comparative analysis of international standards for the fatigue testing of posterior spinal fixation systems: the importance of preload in ISO 12189 / L. La Barbera, C. Ottardi, T. Villa // The Spine Journal. - 2015. - Vol. 15, no. 10. - P. 2290-2296.

A finite element model of the L4-L5 spinal motion segment: biomechanical compatibility of an interspinous device / P. Vena, G. Franzoso, D. Gastaldi, R. Contro, V. Dallolio // Computer Methods in Biomechanics and Biomedical Engineering. - 2005. - Vol. 8, no. 1. - P. 7-16.

Упругая линейная, билинейная, нелинейная экспоненциальная и гиперупругие модели кожи / С.А. Муслов, С.С. Перцов, Е.А. Чижмаков, Н.Б. Асташина, В.Н. Никитин, С.Д. Арутюнов // Российский журнал биомеханики. - 2023. - Т. 27, № 3. - С. 89-103.

Nori, F. Stress analysis of the scoliosis disorder / F. Non, S.H. Ghasemi // Journal of Structural Engineering and GeoTechniques. - 2021. - Vol. 11, no. 1. - P. 1-12.

Effect of the screw type (S2-alar-iliac and iliac), screw length, and screw head angle on the risk of screw and adjacent bone failures after a spinopelvic fixation technique: a finite element analysis / J.K. Shin, B.Y. Lim, T.S. Goh, S.M. Son, H.S. Kim, J.S. Lee, C.S. Lee // PloS One. - 2018. Vol. 13. - P. E0201801.

Childhood obesity as a risk factor for bone fracture: a mechanistic study / J.E. Kim, M.H. Hsieh, B.K. Soni, M.   Zayzafoon, D.B. Allison // Obesity. - 2013. - Vol. 21, no 7. - P. 1459-1466.

Faulkner, K.G. Effect of bone distribution on vertebral strength: assessment with patient-specific nonlinear finite element analysis / K.G. Faulkner, C.E. Cann, B.H. Hasegawa // Radiology. - 1991. - Vol. 179, no. 3. - P. 669-674.

Kinematic and biomechanical responses of the spine to distraction surgery in children with early onset scoliosis: a 3D finite element analysis / B. Pei, D. Lu, X. Wu, Y. Xu, C. Ma, S. Wu // Frontiers in Bioengineering and Biotechnology. - 2022. - Vol. 10. - P. 933341.

Quantification of segmental flexibilities of juvenile lumbar spinal column using a three-dimensional finite element model (FEM) / D.D. Jebaseelan, C. Jebaraj, N. Yoganandan, S. Rajasekaran // 6th World Congress of Biomechanics (WCB 2010), Singapore, August 1-6, 2010. - Berlin, 2010. - P. 525-528.

Fan, W. Stress analysis of the implants in transforaminal lumbar interbody fusion under static and vibration loadings: a comparison between pedicle screw fixation system with rigid and flexible rods / W. Fan, L.X. Guo, D. Zhao // Journal of Materials Science: Materials in Medicine. - 2019. Vol. 30. - P. 1-10.

Development, validation, and application of ligamentous cervical spinal segment C6-C7 of a six-year-old child and an adult / Z. Li, G. Song, Z. Su, G. Wang // Computer Methods and Programs in Biomedicine. - 2020. - Vol. 183. - P. 105080.

Конечно-элементный   анализ напряженнодеформированного  состояния  эндопротеза тазобедренного сустава при двухопорном стоянии / А.И.       Боровков, Л.Б.  Маслов,  М.А.   Жмайло,  И.А.  Зелинский, И.Б.  Войнов,  И.А.       Керестень,  Д.В.  Мамчиц, Р.М.  Тихилов,  А.Н.  Коваленко, С. Билык, А.О. Денисов // Российский журнал биомеханики. - 2018. - Т. 22, № 4. - С. 437-458.

Banu, P.S.N. Microstructure evaluation and modelling the tensile strength and yield strength of titanium alloys / P.S.N. Banu, S.D. Rani // International Journal of Microstructure and Materials Properties. - 2019. - Vol. 14, no. 1. - P. 14-27.

Biomechanical analysis of 4 types of pedicle screws for scoliotic spine instrumentation / X. Wang, C.E. Aubin,

Crandall, S. Parent, H. Labelle // Spine. - 2012. - Vol. 37, no. 14. - P. E823-E835.

Анализ причин дестабилизации металлоконструкции при коррекции врожденной деформации позвоночника у детей младшей возрастной группы / Д.Н. Кокушин, С.В. Виссарионов, М.А. Хардиков, Н.О. Хусаинов,  Н.          Филиппова, В.В. Ильин // Ортопедия, травматология и восстановительная хирургия детского возраста. - 2020. - Т. 8, № 1. - C. 15-24.

Ohrt-Nissen, S. Choice of rods in surgical treatment of adolescent idiopathic scoliosis: what are the clinical implications of biomechanical properties? - a review of the literature / S. Ohrt-Nissen, B. Dahl, M. Gehrchen // Neurospine. - 2018. - Vol. 15, no. 2. - P. 123-130.

Авторы :

А.А. Сафронова, М.А. Жмайло, Л.Б. Маслов, А.И. Боровков, С.В. Виссарионов

Санкт-Петербургский политехнический университет Петра Великого, Санкт-Петербург, Российская Федерация

Ивановский государственный энергетический университет им. В.И. Ленина, Иваново, Российская Федерация

Национальный медицинский исследовательский центр детской травматологии и ортопедии имени Г.И. Турнера, Санкт-Петербург, Российская Федерация


Теги: деформации позвоночника
234567 Начало активности (дата): 07.10.2025
234567 Кем создан (ID): 989
234567 Ключевые слова:  врожденные деформации позвоночника, транспедикулярная фиксация, биомеханическое моделирование, напряженнодеформированное состояние, цифровое моделирование сколиоза, конечно-элементный анализ, коррекция искривления позвоночника
12354567899