Анализ устойчивости к автоколибаниям на субгармонических частотах импульсных источников тока программируемой формы

08.05.2017

Анализ устойчивости к автоколибаниям на субгармонических частотах импульсных источников тока программируемой формы

Методом точечных отображений определены границы областей устойчивости к автоколебаниям на субгармонических частотах в одноконтурной системе управления источника тока с ПИ-регулятором,ШИП с ШИМ2 и индуктивным сглаживающим фильтром.

Методом точечных отображений определены границы областей устойчивости к автоколебаниям на субгармонических частотах в одноконтурной системе управления источника тока с ПИ-регулятором,ШИП с ШИМ2 и индуктивным сглаживающим фильтром.

В работе рассматривается импульсивный источник  тока с замкнутой одноконтурной системой автоматического регулирования
(САР) тока, структурная схема и временные диаграммы работы которой представленны на рис. 1

САР содержит пропорционально-интегральный регулятор тока (РТ) с коэффициентом передачи К_п и постоянной времени интегрирования Т_и ; широтно-импульсный модулятор (ШИМ), реализующий широтно-импульсную модуляцию второго рода (ШИМ-2) и построенный на основе генератора опорного напряжения (ГОН) и компараторов; индуктивный сглаживающий фильтр (Ф) с постоянной времени Тф и статическим коэффициентом передачи Кф ; датчик тока (ДТ) с коэффициентом передачи К_дт.

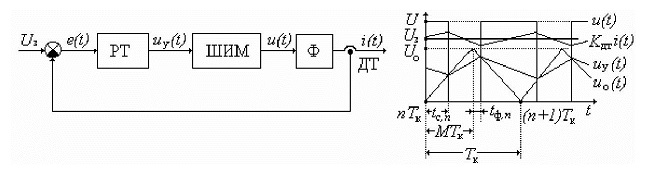
Рис. 1. Структурная схема и временные диаграммы работы САР

РТ преобразует сигнал ошибки e(t) = Uз - К_wi(t) , где U₃ - сигнал задания тока i(t), в сигнал управления и_у(t). ГОН формирует опорный сигнал  и_о (t) пилообразной формы с амплитудой U₀, периодом Т_к и глубиной модуляции М (0 <M < 1) [1].

Выходной сигнал ШИМ u(t) представляет собой последовательность прямоугольных импульсов с амплитудой U, срез и фронт которых на и-м периоде Т_к формируются в моменты времени t_{c n} и tф _n соответственно.

Возможны различные режимы работы САР. Нормальным (основным) является режим вынужденных колебаний с периодом Т_к ,
задаваемым ГОН. Особыми являются режимы вынужденных колебаний с периодом, не равным Т_к. Характерными особыми режимами для САР с ШИМ-2 являются режим автоколебаний на субгармонических частотах и скользящий режим.

Обзор работ, посвященных анализу и синтезу САР с ШИМ-2, позволяет сделать вывод о том, что в них эти диапазоны ограничиваются либо условиями устойчивости к автоколебаниям на субгармонических частотах, либо условиями отсутствия скользящего режима. Так, например, в работе [2] предложена методика параметрического синтеза рассматриваемой САР, заключающаяся в таком выборе значений Тф и К_п , чтобы при заданных значениях Т_к, U₃,М = 0.5 и условии Т_и = Тф обеспечить требуемое быстродействие САР и максимально допустимый уровень пульсаций тока i(t).

При этом выбор значения К_п, определяющего быстродействие САР,ограничен только условиями отсутствия скользящего режима, а устойчивость к автоколебаниям на субгармонических частотах не рассмотрена. Следует отметить, что под условиями устойчивости системы к автоколебаниям на субгармонических частотах специалисты, занимающиеся динамикой систем с вентильными преобразователями, понимают на самом деле условия, при которых такие колебания не возникают [1, 3]. В работе [4] выбор значения К_п ограничен только условиями устойчивости к автоколебаниям на субгармонических частотах, поскольку возникновение скользящего режима исключено за счет введения дополнительных узлов в ШИМ, в частности ^-триггера.

Необходимо отметить, что подобное схемотехническое решение может быть реализовано лишь при М = 0 или М = 1.

Необходимо также отметить, что САР с ШИМ-2 при М = 0.5 обладает лучшими динамическими характеристиками,чем при М = 0 или М = 1 [1]. Таким образом, вопрос о выборе параметров САР с учетом как условий устойчивости к автоколебаниям на субгармонических частотах, так и условий отсутствия скользящего режима при 0 < M < 1 является актуальным.

Задачей данной работы является определение областей устойчивости рассматриваемой САР к автоколебаниям на субгармонических частотах и областей отсутствия скользящего режима.

Динамические процессы в САР описываются уравнениями

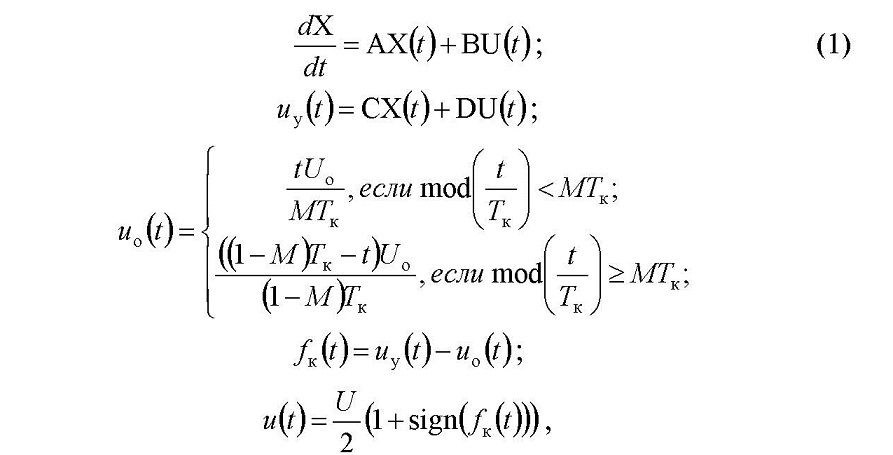
где x(t) = [/(t); u_H (t)]^T - вектор состояния линейной непрерывной части (ЛНЧ) САР; u_H (t) - интегральная составляющая сигнала
управления u_у(t); U(t)= [u(t); U₃]^T - вектор внешних воздействий на ЛНЧ; /к (t) - коммутационная функция; A, B, C и D - матрицы коэффициентов:

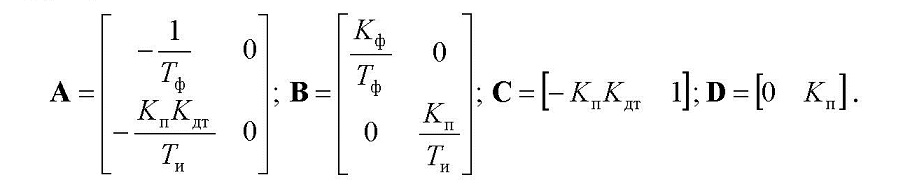
Границы областей отсутствия скользящего режима, полученные из условий

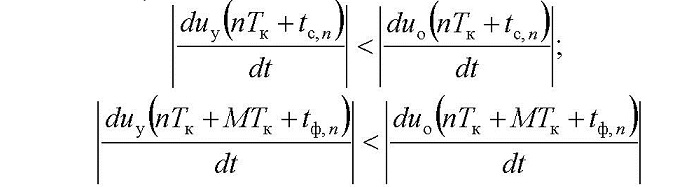
[1, 2], для рассматриваемой САР определяются неравенством

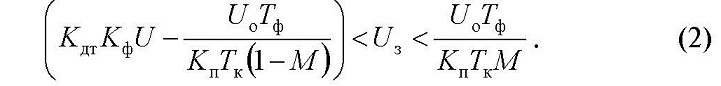
Для обеспечения устойчивости к автоколебаниям на субгармонических частотах необходимо и достаточно, чтобы все собственные числа матрицы Якоби отображения САР в простой неподвижной точке последнего, соответствующей нормальному режиму работы САР, были по модулю меньше единицы [5]. Для определения границ устойчивости рассматриваемой САР к автоколебаниям на субгармонических частотах необходимо, следовательно, получить выражения, задающие отображение, систему уравнений для вычисления значений координат простой неподвижной точки и уравнение для вычисления значений собственных чисел матрицы Якоби.

Решение уравнения (1) на каждом из временных интервалов периода Т_к имеет вид

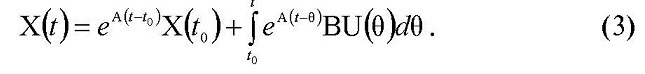
Перепишем (3) в виде

где F(t)= e^A - фундаментальная матрица ЛНЧ; V(t)=jF(t-0)0B -^to матрица, учитывающая влияние вектора u(t) на решение уравнения (1):

Подставляя в (4) t_o = пТ_к, получаем решение уравнения (1) на интервале нТ_к < t < нТ_к + t_{c n}, где u(t) = U , в виде

X(t )= F(t - пТ_к )х(пТ_к ) + V(t - пТ_к )и(пТ_к ). (5)

Подставляя в (4) t_o = пТ_к + t_{c п} , получаем решение уравнения (1) на интервале пТ_к + t_c, _п < t < пТ_к + МТ_К + t_{fc п}, где u(t) = o , в виде X(t)= F(t -(пТк + tc, п МГ + tc, п )+ V(t -(пТк + tc, п ))и(пТк + tc, п ).

Подставляя в (4) t₀ = nT_K + MT_K +tj _n, получаем решение уравнения (1) на интервале пТ_к + МТ_к +tj _n < t < (n + l)T_K, где u(t) = U , в виде ^{X(t )}= ^{F(t -(nT}K + ^MTk + ^tф, n ^))x(nTK + ^MTK + ^, n ⁾+ (7)+ v(t-(nTK + MTk + tj,n))u(nTK + MTk + tj,n) 

Подставляя t = nT_K +1_{c n} в (5), получаем разностное уравнение x(nTK + t_c>n)= F(t_c, n)x(nTK)+ V(t_c, n)u(nTK) . (8)

Подставляя t = nT_K + MT_K + tj _n в (6), получаем разностное уравнение

^x(nTK + ^MTK + ^tj, n ⁾= ^F(MTk + ^tj, n ^{- t}c, n ^)x(nTK + ^tc, n ⁾ + ^v(mTk + ^tj, n ^{- t}c, n⁾U^(nTK + ^tc, n )

Подставляя t = (n + l)T_K в (7), получаем разностное уравнение X((n + 1)Tk)= F((l-M)Tk -tj, n)x(nTK + MTk + tj,n)+ _(1Q)

+ v((l -M)Tk - tj, n )u(nTK + MTk + tj, n ^ ^{( )}

Подставляя (8) в (9), получаем разностное уравнение

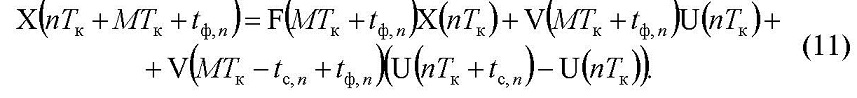
Подставляя (11) в (10), получаем разностное уравнение состояния ЛНЧ САР

x((n + 1)Tk ) = f (x(nTK ))= F(Tk )x(nTK ) + v(Tk )u(nT_K ) + v((l -M)Tk - tj, n)(u(nTK + MTk + tj, n )-u(nTK - tc, n ))- (12)

- v(Tk - tc, nXu(nTK)-u(nTK - tc, n))

Исходя из условия f_K (nT_K + t_{c n})= 0 с учетом (8), получаем нелинейное уравнение для вычисления значения t_c

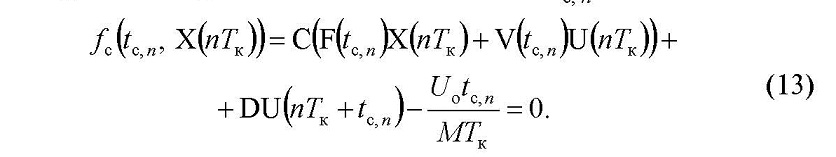
Исходя из принципа действия ШИМ-2, значения t_{c n} и tф _n не могут быть отрицательными и ограничены «сверху»:

0 < t_c, n < MTk ; 0 < t_fc n <(l -M)Tk . (15)

При введении обозначений

X((n + 1)Tk ) = X; X(nTK ) = X; t_c,_n = t_c; tф,n = tф ;

U(nTK) = u(nTK + MTk + t_fc n)=[U,Uз]^T = U_и; u(nTK -t_c,n)=[0,U]^T = U_n

выражения (12)-(15) примут вид

X = f(Tk )x + v(Tk )Uи + (v((l - M)Tk - tф)- v(Tk - tc ))(Uи - U_n); (16.1)

fc(tc, X)= C(F(tc)X + V(tc)Uи) + DU_n -= 0 ; (16.2)

^MTk

fф (tc, tф, X) = c(f(mTk + tф )x + v(mTk + tф )Uи - V⁽MTk - tc + tф )⁽Uи - U_n ⁾⁾+ DUи - ^U° ⁽⁽(₁-^MM)^ ~ '^{ф )} = 0; ⁽¹⁶'³⁾

Совокупность выражений (16) представляет собой нелинейное двумерное отображение первого порядка, заданное неявно.

Значения координат простой неподвижной точки [х*,t_c *, tф * ] находятся в результате решения системы нелинейных ал-
гебраических уравнений

f(Tk )х* - х* + v(Tk )U и + (v((l - м )Tk - tф *)-v(Tk - tc * Ж - U_n ) = 0;

C(F(tc * )X* + V(tc * )Uи) + DU_n - = 0;

c(f(mTk + tф * )x*+v(mTk + tф * )Uи - v(mTk - tc * + tф * )(Uи - U_n))+

U° ((l - м )t_k - t_ф *)+ DU - ° ^{к ф}- = 0,

^и (l - м )Tk

полученной подстановкой X = X = X*, t_c (X*) = t_c *, t, (t_c *, X*) = t, *в (16).

Уравнение для вычисления матрицы Якоби J имеет вид

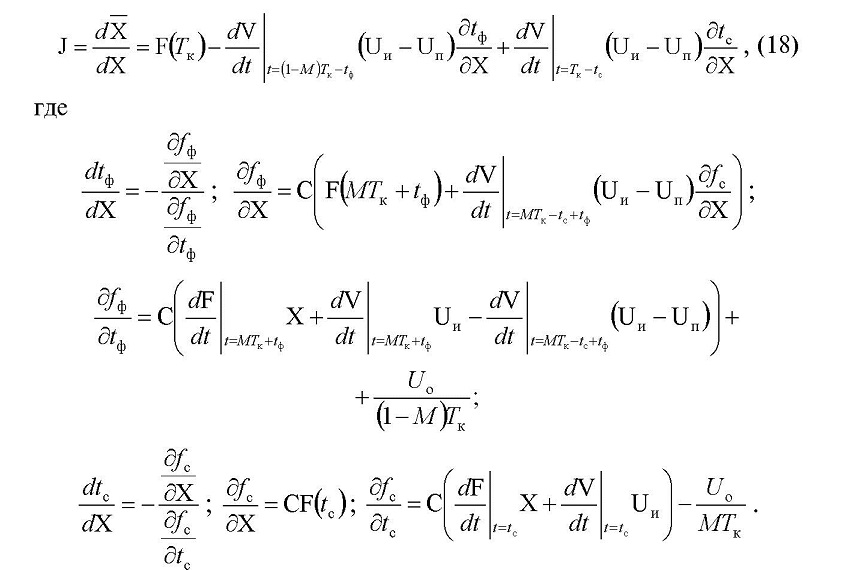
Анализ собственных чисел матрицы Якоби (18) в простой неподвижной точке (17) показал, что при значениях параметров САР,выбранных с учетом условия отсутствия скользящего режима (2),все эти числа по модулю меньше единицы.

Следовательно, при выборе значений параметров САР с учетом условия отсутствия скользящего режима, обеспечиваются и условия устойчивости к автоколебаниям на субгармонических частотах.

Литература

1. Белов Г. А. Полупроводниковые импульсные преобразователи постоянного напряжения: Учеб. пособие. - Чебоксары: Изд-во Чуваш. ун-та,1994. - 96 с.

2. Глазенко Т. А., Синицын В. А., Толмачев В. А. Сравнительный анализ динамических характеристик транзисторных широтно-импульсных преобразователей // Электротехника. - 1988. - № 3. - С. 70-75.

Теги: автоколибания, импульсные частоты, ток, матрица Якоби, уравнения
234567 Начало активности (дата): 08.05.2017 12:14:00
234567 Кем создан (ID): 645
234567 Ключевые слова:  автоколибания, импульсные частоты, ток, матрица Якоби
12354567899